2017年12月27日 星期三

Leetcode 程式解題基礎：linked list 和 binary tree

於
標籤：
 

這篇主要是 linked list 和 binary tree 的程式解題小技巧彙整。

這些題目都很基礎不鑽牛角尖，主要功用是維持一種「程式的手感」；一次就寫出 bug-free 的程式碼是很不容易的，需要一段時間練習。

網路上有很多 online judgment 網站，Accept 之後的成績表可以看一下，盡量會最快的方法，可以看一下討論區的討論，迴圈解、遞迴解、數學解、Botton-up approach、Top-down approach ... 有很多可讀性很高又很短的程式碼，很值得學習：）




一、linked list



1. Dummy node trick


第一個要介紹的是 dummy node trick，dummy node 是為了解決 linked-list 中刪除 head 不便的問題，是非常常見的一個 trick。例如像下面的範例：

Remove Linked List Elements
https://leetcode.com/problems/remove-linked-list-elements/description/

class Solution {
public:
    ListNode* removeElements(ListNode* head, int val) {
        ListNode* dummyNode = new ListNode(0); // dummy node trick
        dummyNode->next = head;
        ListNode* cur = dummyNode;
    
        while(cur->next!=NULL){ // Keeping prev node is a good way to implement delete operator.
            if(cur->next->val==val)
                cur->next = cur->next->next;
            else
                cur = cur->next;
        }
        
        return dummyNode->next; // Don't return head because of special case
    }
};




2. Reverse Linked List


接下來將 linked list 前後反轉 (reverse) 的寫法，有助於提升對 linked-list 操作的熟練度。

Reverse Linked List
https://leetcode.com/problems/reverse-linked-list/description/

class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        ListNode *pre=NULL, *cur=head, *temp=NULL;
       
        while(cur!=NULL){
            temp = cur->next;
            cur->next = pre;
            pre = cur;
            cur = temp;
        }
       
        return pre;
    }
};


程式可以搭配圖片閱讀：



reverse linked list 美圖 (Chiu CC 製)


3. fast-slow pointer trick


fast-slow pointer trick 有以下功能：

  • 沒有 cycle 時，可以尋找此 linked-list 中點
  • 有 cycle 時，fast pointer 和 slow pointer 兩者重合。

Linked List Cycle II
https://leetcode.com/problems/linked-list-cycle-ii/description/

class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        if(head==NULL) return NULL;
        if(head->next==NULL) return NULL;
     
        ListNode *fast=head, *slow=head; // fast-slow pointer trick
        while(fast->next!=NULL && fast->next->next!=NULL){
            fast = fast->next->next;
            slow = slow->next;
            if(fast==slow) return checkPos(head, fast); // fast-slow pointer 重合。
        }
     
        return NULL;
    }
 
    ListNode* checkPos(ListNode* head, ListNode* fast){
        while(head!=fast){ // 會面點到 cycle begin 和 head 到 cycle begin 距離相同。
            head = head->next;
            fast = fast->next;
        }
        return fast;
    }
};





二、Binary Tree



1. Invert Binary Tree


遞迴暖身題，這題因為 homebrew 作者 Max Howell 的吐槽紅了一陣子，答案用簡單的遞迴就可以完成：）

Google: 90% of our engineers use the software you wrote (Homebrew), but you can't invert a binary tree on a whiteboard so fuck off.

原推文連結

class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if(!root) return root;
     
        TreeNode* temp = root->left;
        root->left = root->right;
        root->right = temp;
         
        invertTree(root->left);
        invertTree(root->right);
     
        return root;
    }
};


2. Balanced binary tree validation

給定一個 binary tree，判斷該 tree 是否為 height-balanced (The depth of the two subtrees of every node never differ by more than 1.)。



Leetcode OJ - Balanced Binary Tree
https://leetcode.com/problems/balanced-binary-tree/


1. Top-down Recursion Approach

直接把 Balanced Binary Tree 的數學定義寫成程式碼，非常直覺。但是 maxDepth() 會一直重複呼叫導致有重複計算的部分。

 Time Complexity : $O(n^2)$
Space Complexity : $O(n)$

 
class Solution {
public:
    bool isBalanced(TreeNode* root) {
        if(root==NULL) return 1;
        else return abs(maxDepth(root->left)-maxDepth(root->right)) <= 1 
                 && isBalanced(root->left) 
                 && isBalanced(root->right);
    }
    int maxDepth(TreeNode* root){
        if(root==NULL) return 0;
        else return max(maxDepth(root->left), maxDepth(root->right)) + 1;
    }
};


2. Bottom-up Recursion Approach

bottom-up 程式碼的順序很重要，當左子樹不平衡時，沒有必要再對右子樹求深度，要馬上 return -1，不可把兩個判斷式寫在一起。

通常一個問題 Top-down 比較容易想像且好解出答案，但是較迂迴的 Bottom-up 想法在複雜度上通常較有優勢；所以看到一個題目用直覺的 Top-down 解出答案後，一定要嘗試看看 Bottom-up 能不能構造出更精巧的演算法：Ｄ

Time Complexity : $O(n)$
Space Complexity : $O(n)$

 
class Solution {
public:
    bool isBalanced(TreeNode* root) {
        if( maxDepth(root)==-1 ) return 0;
        else return 1;
    }
    int maxDepth(TreeNode* root){
        if(root==NULL) return 0;
        
        int leftDepth = maxDepth(root->left);
        if(leftDepth == -1) return -1;
        
        int rightDepth = maxDepth(root->right);
        if(rightDepth == -1) return -1;
        
        if(abs(leftDepth-rightDepth) <= 1) return max(leftDepth, rightDepth)+1;
        else return -1;
    }
};



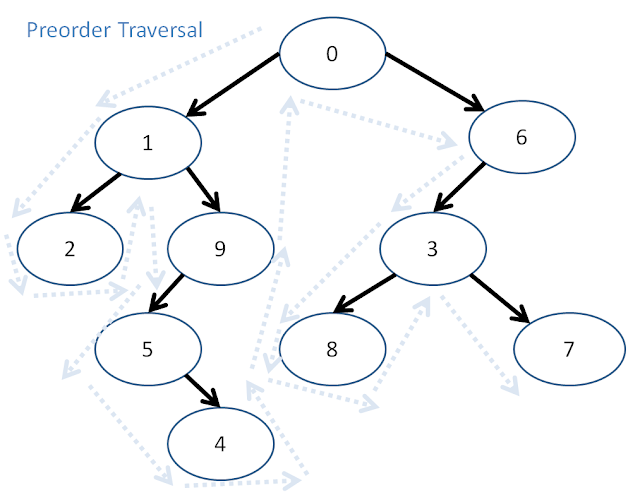
3. Binary tree inorder traversal


這題非常經典，recursion 和 iteration 是很基礎的 traversal binary tree 方法；而 Morris traversal 則是用到了 thread binary tree 的結構。

Binary Tree Inorder Traversal
https://leetcode.com/problems/binary-tree-inorder-traversal/description/


1. Recursive Approach

最直觀的方法，preorder、inorder 和 postorder 遞迴解。

class Solution {
public:
    vector<int> inorderList, temp;
    vector<int> inorderTraversal(TreeNode* root) {
        if(!root) return temp;
        inorderTraversal(root->left);
        inorderList.push_back(root->val);
        inorderTraversal(root->right);
        return inorderList;
    }
};


2. Iterating method using Stack

用 iteration 解時通常會使用一個 stack，也是很基礎的寫法。 (其實 recursion 執行時也使用了 memory stack。)

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> inorderList;
        vector<TreeNode*> stack;
        TreeNode* curNode = root;
     
        while( curNode || !stack.empty() ){
            if(curNode){
                stack.push_back(curNode);
                curNode = curNode->left;
            }
            else{
                TreeNode* popNode = stack.back();
                stack.pop_back();
                inorderList.push_back(popNode->val);
                curNode = popNode->right;
            }
        }
     
        return inorderList;
    }
};


3. Morris traversal using thread binary tree

 這個方法比較特別，用到了葉節點的 null pointer，可以實現 iteration 版本空間複雜度 O(1) 的 traversal。

 
class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        TreeNode* curNode = root;
        vector<int> nodeList;
     
        while(curNode){
            if (!curNode->left){
                nodeList.push_back(curNode->val);
                curNode = curNode->right;
            }
            else{
                TreeNode* pred = curNode->left;
                while (pred->right && pred->right!=curNode)
                    pred = pred->right;
                if(!pred->right){
                    pred->right = curNode;
                    curNode = curNode->left;
                }
                else {
                    pred->right = NULL;
                    nodeList.push_back(curNode->val);
                    curNode = curNode->right;
                }
            }
        }
        return nodeList;
    }
};




小結


大多的題目都能用這些 trick 變化一下解開，如 Palindrome Linked List，解法如下：

  • 快慢指針找中點
  • in-place 的 inverse link-list 方法
  • 比較前後半 list 是否相同

另外還有一些細節，如 DP table 掃 index 的方式、動態陣列 ... 等等不勝枚舉，臨場遇到就要靠清楚的頭腦了：）





References


Chiu CC - Linked List: 新增資料、刪除資料、反轉
http://alrightchiu.github.io/SecondRound/linked-list-xin-zeng-zi-liao-shan-chu-zi-liao-fan-zhuan.html

soulmachine - Leetcode 題解
https://github.com/soulmachine/leetcode

siddontang - Leetcode 題解
https://siddontang.gitbooks.io/leetcode-solution/content/

Leetcode Clean Code Handbook - Edition 1





技術提供：Blogger.
 
© 2023 Mr. Opengate