下推自動機 (Pushdown automaton, PDAs)
下推自動機是包含一個長度不受限制的堆疊的有限自動機。一個下推自動機是含有6個元素的 6-tuple$(Q,\Sigma,\Gamma,\delta,q_0,F)$ ,意義分別是 (狀態集$Q$, 輸入字母集$\Sigma$,堆疊字母集$\Gamma$, 轉移函式$\delta$, 開始狀態$q_0$, 結束狀態$F$)
原文定義如下:
A pushdown automaton is a 6-tuple $(Q,\Sigma,\Gamma,\delta,q_0,F)$, where $Q$, $\Sigma$, $\Gamma$, and $F$ are all finite sets, and
- $Q$ is the set of states;
- $\Sigma$ is the input alphabet;
- $\Gamma$ is the stack alphabet;
- $\delta : Q \times \Sigma_\varepsilon \times \Gamma_\varepsilon \rightarrow P(Q \times \Gamma_\varepsilon)$ is the transition function;
- $q_0 \in Q$ is the start state;
- $F \subseteq Q$ is the set of accept states.
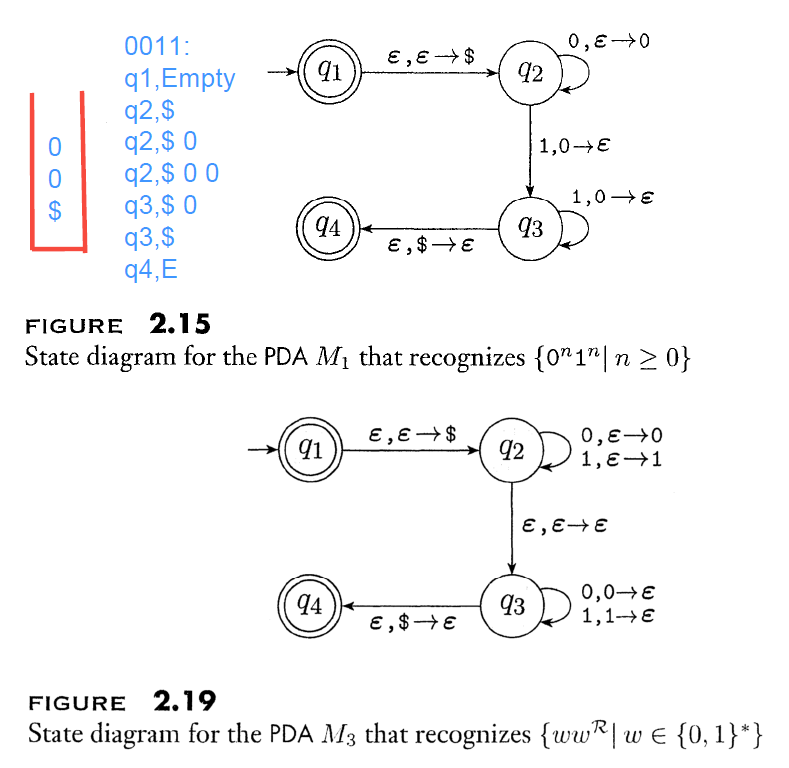
看一個例子最容易理解:
- $a,b \rightarrow c$ 代表的意思是 :
[新吃進來的符號] , [堆疊最上的符號] $\rightarrow$ [放進堆疊的符號] - \$:當作堆疊是否為空的判斷
CFGs和PDAs等價
我們要證明CFGs和PDAs等價,也就是任找一個CFGs我們都可以找到一個PDAs使兩者recognize的language相同,反之亦然。
CFGs 轉 PDAs
在堆疊最上面的符號,只有兩種轉移方式
- 對於變數符號 $A$, 將換成的新字串反向推入堆疊 : $\varepsilon,A \rightarrow w$ (如下圖紅色部分)
- 對於終止符號 $a$, 和輸入配對 : $a,a \rightarrow \varepsilon$ (如下圖黃色部分)
看一個例子最容易理解:
PDAs 轉 CFGs
- $V = \{A_{pq}\ |\ p,q \in Q\}$ //所有state的配對
- $S = A_{q_0,q_{accept}}$
- $R$ contains the following three sets of rules:
- For each $p, q, r, s \in Q$, $t \in \Gamma$, and $a, b \in \Sigma_\varepsilon$, if$(r, t) \in (p, a, \varepsilon)$ and $(q, \varepsilon) \in \delta(s, b, t)$, the rule
$A_{pq} \rightarrow aA_{rs}b$ - For each $p, q, r \in Q$, the rule
$A_{pq} \in A_{pr}A_{rq}$ - For each $p \in Q$, the rule
$A_{pp} \rightarrow \varepsilon$
看一個例子最容易理解:
Reference
交大陳穎平教授正規語言講義