Chapter 4 Graph Algorithm
4.1 Minimum Spanning Trees
- Spanning Tree
- 定義
- S = (V, F)為G的一個Spanning Tree且S滿足
- 自F’中任取一邊加入S中必形成Cycle
- 在S中任何頂點對之間必存在一唯一Simple path
- 性質
- 若G 不連通則G無Spanning Tree
- G中的Spanning Tree不只一個
- 同一G中的任二個不同之Spanning Tree不一定有交集的邊存在
- Minimal Spanning Tree
- 定義
- 在G 的所有Spanning Tree中,具有最小的邊成本總和者。
- 可求MST的演算法如下
- Kruskal’s Algorithm:下一段詳述。
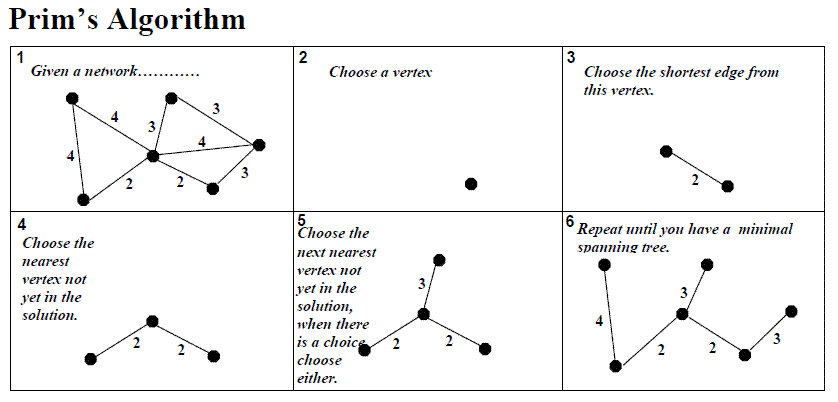
- Prim’s Algorithm:從一個點出發( U, V-U ),像Dijkstra,由擴張樹的某一頂點與其它頂點的所有邊中挑選出具最小值者,不允許有迴路,O(n^2),使用資料結構Heap優化,O(ElgV)。
- Sollin’s Algorithm:以merge的概念實作,剩一棵樹結束
- 皆是greedy algorithm。
- Kruskal’s Algorithm
- 概念
- Kruskal演算法是一種用來尋找最小生成樹的演算法,是greedy演算法的應用。Kruskal演算法是以增加邊的觀念做為出發點。首先將所有的邊,依照權重的大小排序。再來依序加入權重最小的邊,如果造成cycle時,則必須捨棄,直到增加了n - 1條邊為止(假設有 n 個節點)。Kruskal演算法在圖中存在相同權值的邊時也有效。
- 步驟
- 選擇:由spanning tree的所有邊中,挑選出具最小值者(不允許有迴路)。
- 重複直到下列任一條件成立為止
- (n-1)個邊已挑出 //n是頂點的個數
- 無邊可挑,若 |F| < n-1,則無spanning tree
- 複雜度分析
- 建邊權重的heap : O(E)
- 取得並刪除最小權重的邊(u,v) : O(logE)
- 需偵測取得的邊是否構成cycle,使用set operation操作,同一集合為同set
- union(u,v) : O(1)
- Find(u) : 花O( a(m,n) ), 逼近O(1)
- 每回合最多花O(logE)
- 因此Kruskal’s Algorithm complexity = O(E) + O(ElogE) = O(ElogE)
- 證明
- 手法為cut-and-paste
- 假設最小權重的邊E不在minimum spanning tree T中
- 在T中加入E會形成cycle
- 因此拿掉一個比E權重大的邊,形成權重較小的T’,矛盾而得證
4.2 Single pair shortest path
- Dijkstra’s Algorithm
- 概念
- Dijkstra’s Algorithm 解決非負邊有向圖的單源最短路徑問題,演算法最終得到一個最短路徑樹。採用Greedy解題策略,為目前已知的最快的單源最短路徑演算法。
- 步驟
- 首先以某一節點當作出發點,在與其相連且尚未被選取的節點裡,選擇加入離出發點距離最短的節點
- 透過新增的節點來Relax到達其他節點的距離。
- 如此重覆加入新節點,直到所有的節點都被加入為止。
- Relax Procedure:cost(A—>C) + cost(C—>B) < cost(A—>B),若我們原本是直接由A走到B,改成A經過C 再走到B,這個過程我們稱為鬆弛(Relax)。
- 複雜度分析
- 選擇加入離出發點距離最短的節點:O(V)*T_extract-min
- Relax到達其他節點的距離:O(E)*T_decrease-key
- Dijkstra’s Algorithm complexity = O(V)*T_extract-min + O(E)*T_decrease-key
- Array : O(V^2)
- Binomial Heap:O(VlogV+ElogV)
- Fibonacci Heap:O(VlogV+E)
- 證明
- Lemma 1: Optimal Substructure:The subpath of any shortest path is itself a shortest path. Proof. Cut and paste
- Lemma 2: Triangle inequality:If δ(u,v) is the shortest path length between u and v, δ(u,v) ≤ δ(u,x) + δ(x,v)
- Theorem 1:Initializing d[s] ← 0 and d[v] ← ∞ for all v ∈V – {s} establishes d[v] ≥ δ(s, v) for all v ∈ V, and this invariant is maintained over any sequence of relaxation steps.
- Proof. Suppose not. Let v be the first vertex for which d[v] < δ(s, v), and let u be the vertex that caused d[v] to change: d[v] = d[u] + w(u, v). Then, d[v] < δ(s, v) (supposition) ≤ δ(s, u) + δ(u, v) (triangle inequality)≤ δ(s,u) + w(u, v) (sh. path ≤ specific path) ≤ d[u] + w(u, v) (v is first violation) Contradiction.
- Theorem 2:Dijkstra’s algorithm terminates with d[v] = δ(s, v) for all v ∈ V
- Proof. Suppose u is the first vertex added to S for which d[u] ≠ δ(s, u). Let y be the first vertex in V – S along a shortest path from s to u, and let x be its predecessor: Since u is the first vertex violating the claimed invariant, we have d[x] = δ(s, x). Since subpaths of shortest paths are shortest paths, it follows that d[y] was set to δ(s, x) + w(x, y) = δ(s, y) when (x, y) was relaxed just after x was added to S. Consequently, we have d[y] = δ(s, y) ≤ δ(s, u) ≤ d[u]. But, d[u] ≤ d[y] by our choice of u, and hence d[y] = δ(s, y) = δ(s, u) = d[u]. Contradiction.
- 證明說明:我們必須證明「當一個點被標記成以拜訪時,它當下距離起點的距離即為最短路徑的長度」。
- 使用反證法證明:若於標記頂點 u 時,起點 s 到該點 u 當下距離 d 不是最短,則必有其他條路徑使得起點到該點 u 的距離比當下的距離 d 更短,再由「最短路徑的子路徑必亦為最短路徑」這個性質可知,若有一條路徑 s→v→u 的長度比 d 更短,則 s→v 的長度必然小於 d,因此
- 情況A — v 尚未被標記:但此情況應該先標記 v 而非 u,故與假設矛盾。
- 情況B — v已被標記:但這種情況u至原點的距離必然已經被Relax成比d還短,故亦矛盾。
- 因此由反證法我們得知,Dijkstra 演算法是正確的。 然而,由於這一點,Dijkstra 演算法並不適用於有負的邊權重的情況。
- Bellman-Ford Algorithm
- 概念
- Bellman-Ford Algorithm解決存在負邊有向圖的單源最短路徑問題,採用Dynamic programming解題策略。在Bellman-Ford和Dijkstra兩個演算法中,計算時每個邊之間的估計距離值都比真實值大,並且被新找到路徑的最小長度替代。
- 步驟
- 不斷的利用邊集合中的邊對目前的最佳路徑作Relax的動作,直到確定各路徑的長度為最短。
- 假設對象的圖不存在負圈,則任意一條最短路徑皆不會經過重複的點,因此最多經過|V|個點,反之必包含負圈。
- 複雜度分析
- 每次Relax須掃過所有邊:O(E)
- 對所有邊進行Relax操作,共|V | − 1次:O(V)
- Bellman-Ford Algorithm complexity = O(VE)
- 相關問題及演算法
- 開放最短路徑優先演算法是該演算法在網路路由中的一個具體實現。
- 與 Dijkstra 演算法不同,Bellman-Ford演算法可用於具有負花費邊的圖,只要圖中不存在總花費為負值且從源點 s 可達的環路(如果有這樣的環路,則最短路徑不存在,因為沿環路循環多次即可無限制的降低總花費)。
- 與最短路徑問題相關最有名的一個問題是旅行商問題,此類問題要求找出恰好通過所有目標點一次且最終回到原點的最短路徑。然而該問題為NP-完全的;換言之,與最短路徑問題不同,旅行商問題不太可能具有多項式時間解法。
- 如果有已知資訊可用來估計某一點到目標點的距離,則可改用A*搜尋演算法,以減小最短路徑的搜尋範圍。
4.3 All Pairs Shortest Paths
- Flord-Warshall Algorithm
- 概念
- Flord-Warshall Algorithm是解決任意兩點間的最短路徑的一種演算法,可以正確處理有向圖或負權的最短路徑問題,同時也被用於計算有向圖的傳遞閉包。
- 步驟
- 利用邊進行Relax搭配Dynamic Programming的方式來對點和點之間的最短距離進行維護及更新。
- 複雜度分析
- 利用三層迴圈來實行動態規劃,以外層的迴圈 k 來枚舉中繼點,內層的 i, j 迴圈來進行鬆弛更新的動作
- 因此Flord-Warshall Complexity = O(V^3)
- Johnson’s algorithm
- 概念
- Johnson’s algorithm是解決任意兩點間的最短路徑的一種演算法,使用Reweight手法,當|E|足夠小時比Floyd-Warshall快。
- 步驟
- Find a vertex labeling h such that ŵ(u, v) ≥ 0 for all (u, v) ∈ E by using Bellman-Ford to solve the difference constraints h(v) – h(u) ≤ w(u, v), or determine that a negative-weight cycle exists.
- Theorem. Given a label h(v) for each v ∈ V, reweight each edge (u, v) ∈ E by ŵ(u, v) = w(u, v) + h(u) – h(v).
- Run Dijkstra’s algorithm from each vertex using ŵ.
- Reweight each shortest-path length ŵ(p) to produce the shortest-path lengths w(p) of the original graph.
- 複雜度分析
- 首先用Bellman-Ford來reweight : O(VE)
- 執行V次Dijkstra : O( V*(E+VlgV) )
- 因此Johnson’s algorithm Complexity = O(VE + V^2 lg V)












.jpg)









沒有留言:
張貼留言